点の移動・回転
目次[非表示] |
座標系
3次元空間を表す(直交)座標系は二種類あるらしい。右手系と左手系。えーと、親指の付け根に原点をとって、親指、人差し指、中指にそれぞれ 、
、 、
、 軸を割り当てると
軸を割り当てると が右回りになるのが右手系、左回りになるのが左手系。
図から分かるように、この二つの座標系はどんなに回転させても一致しないので無駄な努力はしない事。右手系と左手系の変換は適当な軸一つまたは三軸全ての符号を反転させればよい。ただし、二つの座標系を一緒に扱うと混乱するだけなので、どちらか一方に統一した方が賢い。まぜるな危険。
ここでは特に断らない限り右手系を用いる事にする。
が右回りになるのが右手系、左回りになるのが左手系。
図から分かるように、この二つの座標系はどんなに回転させても一致しないので無駄な努力はしない事。右手系と左手系の変換は適当な軸一つまたは三軸全ての符号を反転させればよい。ただし、二つの座標系を一緒に扱うと混乱するだけなので、どちらか一方に統一した方が賢い。まぜるな危険。
ここでは特に断らない限り右手系を用いる事にする。
3次元の回転は「どれだけ回したか」の他に「どの軸周りに回したか」というのも必要。なので、回転軸と回転角を適当に定める必要がある。 ここでは図に示すように、右手系は右ネジの向き、左手系は左ネジの向きに軸と回転方向をとる。こうすると2次元の回転方向と(z軸周りの)回転方向が同じになるため、何かと考えやすいはず。
2次元の点の移動と回転
いわゆる座標変換の話。ここで注意するのは、どの座標系からどの座標系への変換なのか、計算して出てきた座標はどの座標系で表されているかという事。ここでは、固定されている座標系から見て原点が にあって
にあって 回転している座標系で表現されている点
回転している座標系で表現されている点 を、もとの固定されている座標系で表すとどうなるか、というのをやる。言い換えると、「ある点
を、もとの固定されている座標系で表すとどうなるか、というのをやる。言い換えると、「ある点 が原点周りに
が原点周りに 回転して、平行移動
回転して、平行移動 しました。この点
しました。この点 はどこでしょう」という問題。
はどこでしょう」という問題。
まあ、これは図を見たまんまで。 とすると、
とすると、 成分はもとの座標系で
成分はもとの座標系で 、
、 は
は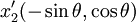 になって
になって 平行移動するので、次式になる。
平行移動するので、次式になる。

このとき、

を回転行列といったりする。この行列は正規直交行列( )で
)で になる。
になる。
複素数を使った回転の表現
2次元の原点周りの回転は、大きさ1の複素数 を使っても表現できる。
を使っても表現できる。

ただし は虚数単位とする。
は虚数単位とする。
で、何が言いたいかというと、「大きさが1」という条件は使いやすいので、覚えておくと良い事あるかもよってこと。
3次元の座標変換
2次元の場合と同じ。原点周りの回転 、平行移動
、平行移動 とすると次式になる。
とすると次式になる。

ただし、 は行列式の値が1の3x3正規直交行列である。
は行列式の値が1の3x3正規直交行列である。
ちなみに、 のものは擬回転と呼ぶ事があり、これは回転の他に右手系・左手系を一方から他方に変換する作用も持つ。
つまり、右手系の話しかしていない時にこのような行列が出てきた場合は、何かがおかしいってこと。
のものは擬回転と呼ぶ事があり、これは回転の他に右手系・左手系を一方から他方に変換する作用も持つ。
つまり、右手系の話しかしていない時にこのような行列が出てきた場合は、何かがおかしいってこと。
逆問題を解く
今までは、移動量や回転角が与えられた場合に点がどう動くかを見てきた。ここでは反対に移動前後の点の組 が与えられた時に、平行移動量および回転角(・回転軸)を求めることを考える。
が与えられた時に、平行移動量および回転角(・回転軸)を求めることを考える。
要するに、次式を満たす を求める。
を求める。

実際には誤差なんかがあって等式は成り立たなくなるだろうから、できるだけ等しくなるような値を求める事にする。
重心に関する運動
とりあえず、 の重心
の重心 を計算してみる。
を計算してみる。

重心を原点にとって とすると、
とすると、

となるから、これから回転 が求められそうだ。
が求められそうだ。
回転が分かれば平行移動成分は次式で計算できる。

特に なら回転と無関係に平行移動成分が分かる。
なら回転と無関係に平行移動成分が分かる。
というわけで、ここからは回転を求める事に精を出す。
2次元の回転
誤差の定義は色々考えられるが、ここではベクトルの内積は同じベクトル同士を掛けた時が最大というのを使って次式を用いる。

これは長いベクトルの方が誤差に表れやすいため、そういうベクトルを重視する人向けの誤差である。

とおいて を未知数
を未知数 に付いて書き直すと以下の式を得る。
に付いて書き直すと以下の式を得る。

この式が の下で最大になるのは当然次の時。
の下で最大になるのは当然次の時。


3次元の回転
まあ、2次元の時と同じ。大きさが1の複素数 の代わりに、大きさが1のクォータニオン
の代わりに、大きさが1のクォータニオン を使うだけ。
を使うだけ。
クォータニオンの成分を

とすると、回転は次式で表される。

で、内積が最大になるようにする、と。

(続きはまたいつか)

